Statistische Toleranzanalyse in der Praxis

Nachfolgend möchten wir Ihnen zeigen, wie Sie einfach und schnell mit Hilfe des Programmsystems simTOL eine statistische Toleranzanalyse durchführen können. Die Vorgehensweise wird am Beispiel einer radialen Dichtung mittels O-Ring erläutert. Es wird deutlich, dass auch ohne den Einsatz komplexer 3D-Simulationswerkzeuge – und ohne dem zu deren Bedienung erforderlichen Expertenwissen – inhaltsstarke und vor allen transparente Ergebnisse ermittelt werden können.

1. Schritt: Was soll berechnet werden?

Sie kennen das, wie muss ich meine Einzelteile tolerieren, damit die Baugruppenfunktion sichergestellt ist. Am Beispiel der radialen statischen äußeren Dichtung mittels O-Ring eines mit Innendruck beaufschlagten Behälters muss die Dichtheit gewährleistet sein. Laut DIN 3771 wird die statische Abdichtung durch die radiale Verpressung des O-Rings herbeigeführt. Die Verpressung sollte 15 bis 30 [%] des Schnurdurchmessers vom O-Ring betragen.

Frage: Kann die erforderliche Verpressung des O-Rings –und damit die Dichtigkeit- prozesssicher erreicht werden?

2. Schritt: Welches sind die geometrischen Eingangsgrößen für die statistische Toleranzberechnung?

Der gezeigte Behälter wird durch einen zu verschraubenden Deckel mit Hilfe eines aufzubringenden definierten Drehmomentes geschlossen. Es wird ein leichter radialer Festsitz des O-Rings auf dem Nutgrunddurchmesser des Deckels gefordert. Dieser Festsitz hat die Forderung d_O-Ring < d_Nutgrund zu erfüllen. Also maximal plus 6 [%] des Innendurchmessers vom O-Ring

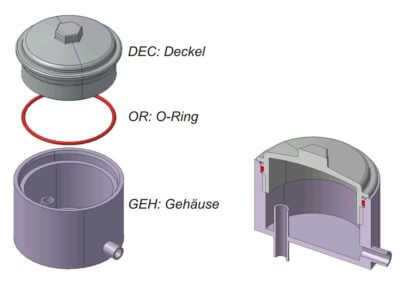
Verschraubter Deckel an einem Druckbehälter

Durch das Anziehen des Deckels kann dieser sich einseitig an den Bohrungsdurchmesser des Gehäuses anlegen. Hierdurch können sich dann als Folge unterschiedliche Nuttiefen ergeben. Die kleinste Nuttiefe t_min tritt dann an der Stelle auf, wo es Kontakt zwischen dem Führungsdurchmesser am Deckel und dem Bohrungsdurchmesser am Gehäuse gibt. Und auf der gegenüberliegenden Seite tritt dann die größte Nuttiefe t_max auf, siehe Abbildung 1.2. Dieser Zusammenhang führt bei der Berechnung des Qualitätsmerkmales (radiale Verpressung) zu einer Fallunterscheidung.

Fall A: Maximale Nuttiefe -> minimale Verpressung

Fall B: Minimale Nuttiefe -> maximale Verpressung

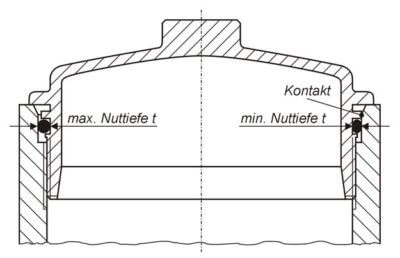
Unterschiedliche Nuttiefen durch das Verschrauben des Druckbehälterdeckels

Für die Toleranzberechnung ist es notwendig, die Einfluss nehmenden Funktionsmaße zu lokalisieren. Für die Durchführung der statistischen Toleranzberechnung mit simTOL wird darüber hinaus jedem relevanten Funktionsmaß (Toleranz) ein Identifizierer, das sogenannte Kurzzeichen, zugeordnet.

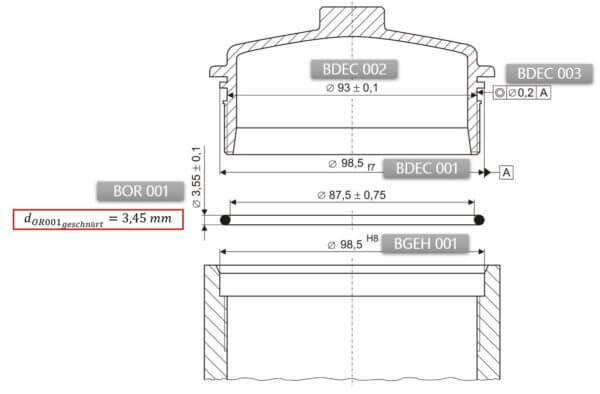
Vermaßte dichtungsrelevante Einzelteile des Druckbehälters (inkl. Kurzzeichen)

Aufgrund der beiden unterschiedlichen Durchmesser von D_O-Ring [87,5 mm] und d_Nutgrund [93,0 mm] wird der O-Ring bei der Montage gestreckt. Hierdurch ändert sich die Länge in der neutralen Faser des O-Rings. Da das Volumen vor und nach der Montage konstant bleibt, ergibt sich unter der Annahme einer homogenen Einschnürung der Schnurdurchmesser des montierten O-Rings von

d_O-Ring = 3,45 [mm] [BOR001]

Hiernach engt sich der Schnurdurchmesser um 0,1 [mm] ein.

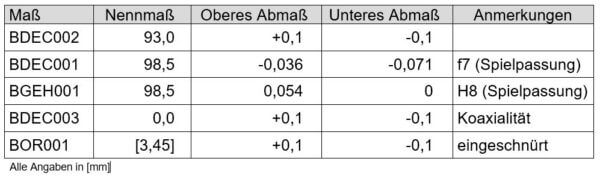
Geometrische Eingangsgrößen

In Nominallage, also ohne die Einflüsse von Toleranzen, lässt sich die (relative) Verpressung P_r des montierten (eingeschnürten) O-Rings rechnerisch ermitteln (die Gleichungen dazu finden Sie in der Druckversion in unserem Downloadbereich). Sie ergibt sich mit

P_r,min = P_r,max= 0,203

Unsere Leistungen im Toleranzmanagement

In Prozent sind das dann 20,3 [%].

3. Schritt: Wie verhält sich das System unter dem Einfluss von Toleranzen?

Wegen der unvermeidlichen Abweichungen in der Teilefertigung werden die geometrischen Größen mit Toleranzen versehen. Die Gleichungen für die Berechnungen der relativen Verpressungen (2 und 3) deuten schon darauf hin, dass die Toleranzen eines jeden Einzelteils nicht direkt, also nicht mit dem Faktor eins, auf die Verpressung wirken. Wie groß der Einflussfaktor (der sog. Linearitätskoeffizient a) tatsächlich ist, kann berechnet werden (Stichwort: Partielle Differentiation). Das Ergebnis dieser Berechnung ist in der nachfolgenden Tabelle dargestellt.

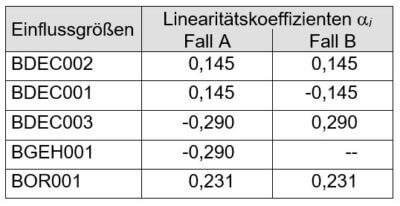
Berechnete Linearitätskoeffizienten

4. Schritt: Die statistische Toleranzberechnung

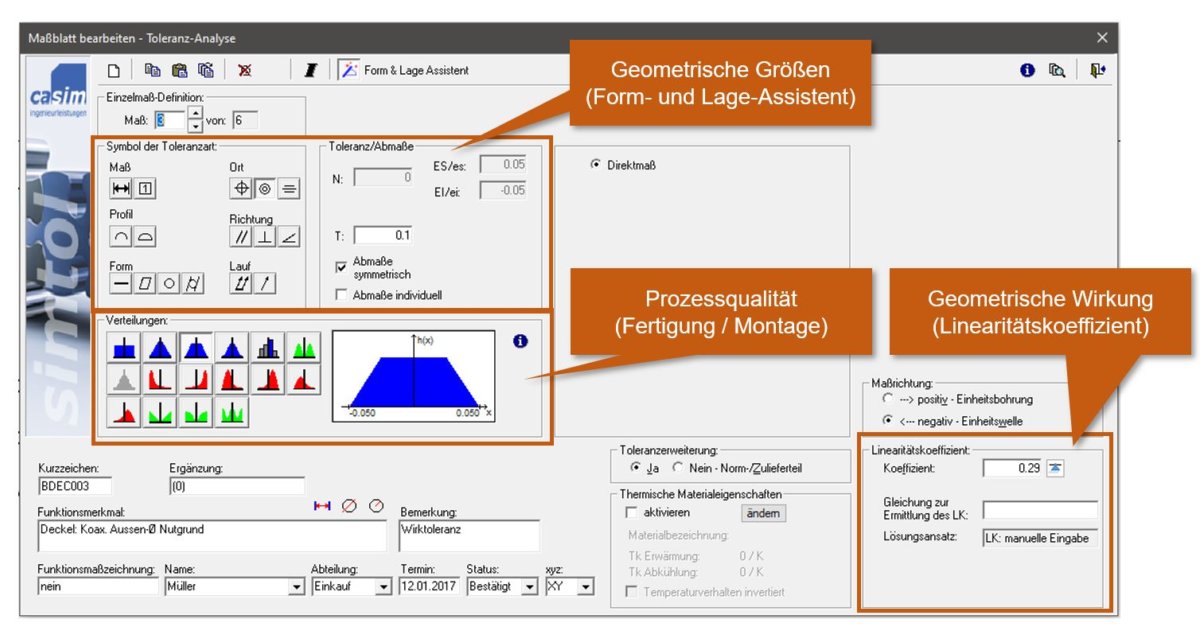
Zur Durchführung einer statistischen Toleranzanalyse müssen neben den geometrischen Eingangsgrößen (Nennmaß, Abmaße, Linearitätskoeffizient) auch die Qualität des Fertigungsprozesses beschrieben werden. simTOL bietet hierfür standardisierte Verteilungstypen an.

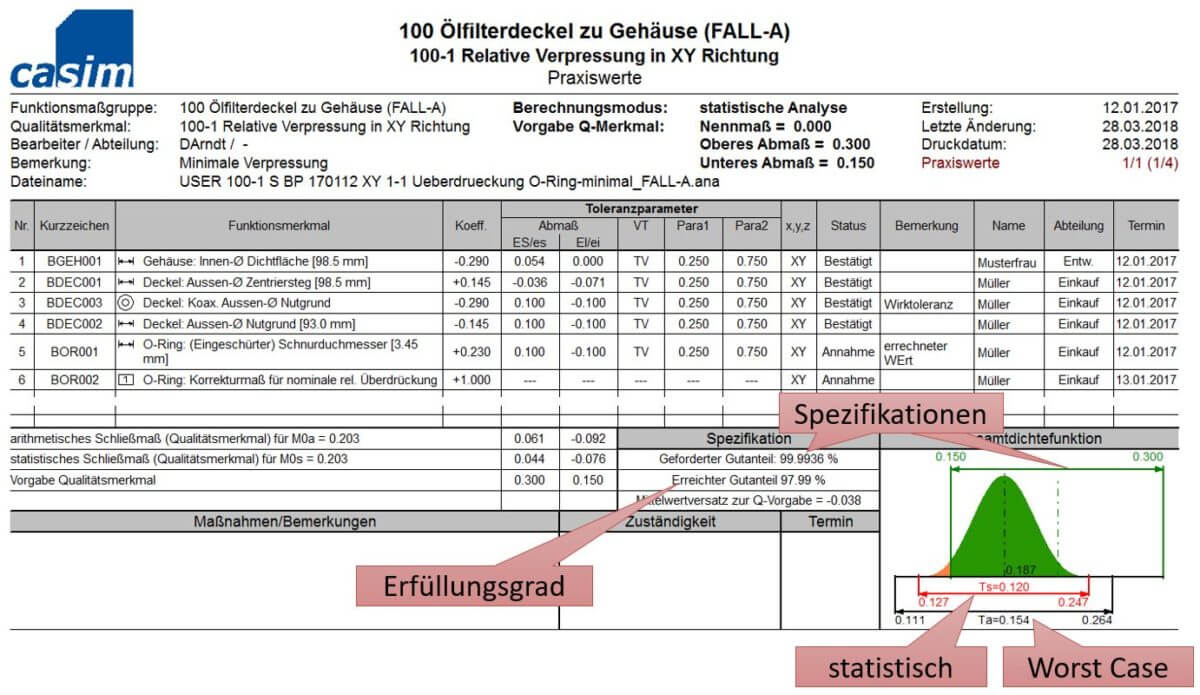
Eingabe der Berechnungsparameter in simTOL (exemplarisch für Koaxialität)

Nach der sukzessiven Eingabe und Parametrisierung der Einflussgrößen kann mit Hilfe von simTOL die resultierende Gesamt-/ Schließmaßtoleranz einer Baugruppenfunktion berechnet werden. Die Ausgabe der Ergebnisse erfolgt über verschiedene Protokolle. Nachfolgend ist das sogenannte Praxiswerte-Protokoll zu sehen. In diesem Protokoll wird in tabellarischer Form dargestellt, welches die Eingangsgrößen sind. Im Fußbereich wird ausgewiesen, welche Ergebnisse hinsichtlich der Schließmaßtoleranz daraus resultieren. Es gibt für die Schließmaßtoleranz einen Ausdruck für das Worst Case- bzw. arithmetische Ergebnis (Ta) und einen für das statistische Ergebnis (Ts). Letzteres basiert auf frei definierbare Qualitätsanforderung (geforderter Gutanteil), hier 99,9936%. Diese Ergebnisse können nun mit den technischen Forderungen bzw. Spezifikationen an die Baugruppenfunktion (im Protokoll grün dargestellt) verglichen werden. Im Zuge dieses Vergleiches ermittelt simTOL die erreichbare Zahl von Baugruppen, die diese Spezifikationen erfüllen – hier sind dies 97,99%.

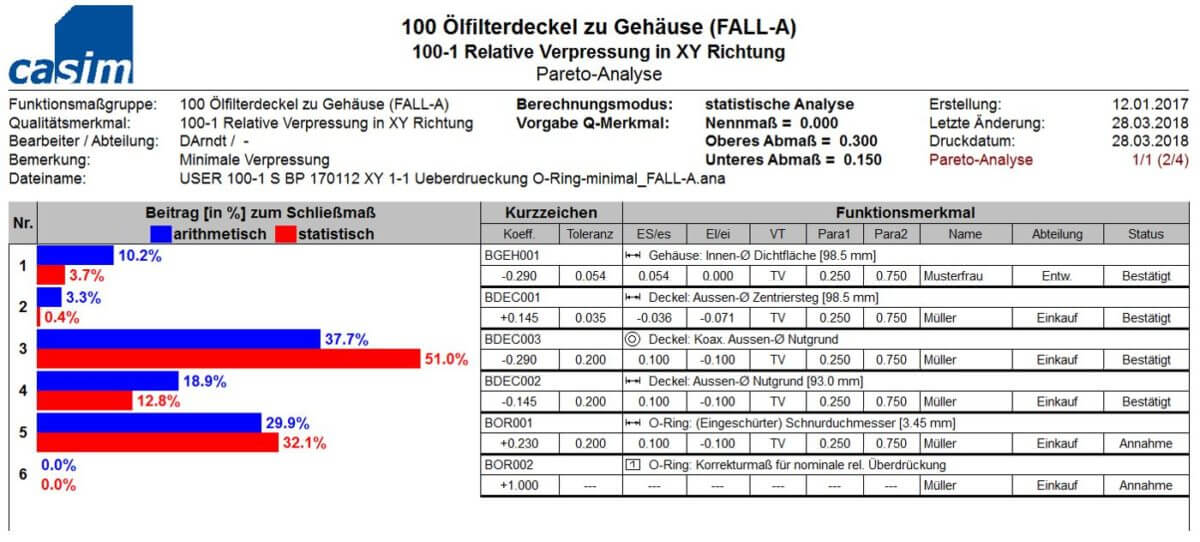
simTOL Praxiswerte-Protokoll: Eingangsgrößen (Toleranzkette) und Berechnungsergebnisse

Mit dem Protokoll Pareto-Analyse wird aufgezeigt, welchen prozentualen Einfluss die einzelnen Maßkettenglieder / Toleranzkettenglieder an der Schließmaßtoleranz haben. Diese Auswertung wird sowohl für die arithmetische, als auch für die statistische Schließmaßtoleranz durchgeführt. So werden bei der statistischen Bewertung neben den geometrischen Einflüssen auch die Prozessqualität, repräsentiert durch die verschiedenen Verteilungstypen, mit einbezogen. Mit diesen Informationen können Optimierungsschritte, sofern erforderliche, gezielt eingeleitet werden.

simTOL-Pareto-Analyse zur Ermittlung der (Haupt-)Beitragsleister für Fall A

5. Schritt: Interpretation der Ergebnisse

Ergebnisbewertung der arithmetischen Toleranzanalyse:

Es liegt eine zu geringe radiale Verpressung bei maximaler Nuttiefe (Fall A) vor. Mit 11,1 [%] relativer Verpressung wird die untere Spezifikationsgrenze deutlich unterschritten. Somit könnte an dieser Dichtungsstelle aus dem Druckbehälter Flüssigkeit austreten. Die andere Extremlage, die maximale Verpressung für den Fall A ist mit 24,7 [%] innerhalb der erforderlichen Grenze und ist somit zunächst unkritisch.

Ergebnisbewertung der statistischen Toleranzanalyse:

Die statistische Toleranzanalyse wurde für eine angestrebte Prozesssicherheit von Cp = Cpk = 1,33, was einer Annahmewahrscheinlichkeit (oder einem Erfüllungsgrad) von 99,9936 [%] entspricht, durchgeführt. In Analogie zu den arithmetischen Ergebnissen ergibt sich damit für die minimale relative Verpressung (Fall A) ein Wert von 12,7 [%]. Ferner wird mit dem erreichbaren Gutanteil ausgewiesen, dass nur 97,99 [%] aller Druckbehälter die technisch erforderlichen Grenzen von minimal 15 [%] bis maximal 30 [%] relativer Verpressung einhalten. Da 0,2236 [%] aller Druckbehälter eine zu geringe relative Verpressung aufweisen, wird die Dichtigkeit zwar in den meisten Fällen, jedoch nicht prozesssicher eingehalten.

In unserem Downloadbereich finden weitere Informationen: