Thermische Einflüsse in statistischen Toleranzberechnungen
Mit Hilfe der statistischen Toleranzanalyse wird berechnet, wie sich die einzelnen Istmaße einer Baugruppe zu einer Gesamtverteilung ergeben. So ist es möglich, schon früh im Entwicklungsprozess zu erkennen, ob beliebige Baugruppenfunktionen (zum Beispiel ein gewünschter Freigang, eine notwendige Lochüberdeckung u.v.m) prozesssicher eingehalten werden können. Die Ergebnisse statistischer Toleranzberechnungen sind somit auch geeignet zu ermitteln, unter welchen Bedingungen und Toleranzanforderungen für die Einzelteile die festgelegten Baugruppenspezifikationen einhaltbar sind.
In den meisten Fällen werden Zusammenbauten basierend auf Nominalgeometrien ausgeführt. Potentielle Abweichungen vom Idealmaß, die ihren Ursprung in den unausweichlichen Streuungen von Fertigungsprozessen haben, werden im Allgemeinen ausschließlich über die entsprechenden Toleranzinformationen in die Berechnung integriert.
Nicht selten unterliegen Baugruppen während des Betriebs relevanten thermischen Belastungen. Für diese Fälle sind die Geometrien aller Einzelteile der Baugruppe in Form der Wärmeausdehnung mit zusätzlichen Einflüssen beaufschlagt. Die Frage bleibt, wie sich die fertigungs- und thermisch bedingten Einflüsse überlagern und welchem Einfluss sie auf die Baugruppenfunktionen ausüben.
Sichere & schnelle Berechnung mit simTOL
Wärmeausdehnung
Die Wärmeausdehnung, auch thermische Expansion genannt, tritt sowohl bei Festkörpern, als auch bei Flüssigkeiten und Gasen auf. Will man dieses Verhalten theoretisch beschreiben und berechnen, gilt es umfangreiche Differentialgleichungen aufzustellen und zu lösen, sowie die notwendigen Informationen für die zugehörigen Variablen bereitzustellen. Nur so besteht die Möglichkeit, für beliebige Geometrien unter Berücksichtigung makroskopischer Abhängigkeiten in ein-, zwei- und dreidimensionaler Richtung umfassende Ergebnisse zu generieren. Bei aller Vollständigkeit eines solchen mathematischen Ansatzes muss jedoch auch der nicht unerhebliche Aufwand in Betracht gezogen werden, diesen umzusetzen. Aus diesem Grunde, werden in der Praxis von Entwicklungsingenieuren Vereinfachungen getroffen, die in eine leicht zu handhabende Berechnungsvorschrift münden.
Vereinfachter Ansatz zur Berechnung der Wärmeausdehnung
Folgende Vereinfachungen werden in der Praxis (zur geometrischen Auslegung von Bauteilen) zur Berechnung der Wärmeausdehnung häufig getroffen:
- Ausschließlich Festkörper (keine Gase oder Flüssigkeiten).
- Längenausdehnung ist isotrop, also in allen Raumrichtungen gleich.
- Konstanter, nicht temperaturabhängiger Längenausdehnungskoeffizienten.
Diese Vereinfachungen führen zu der sehr bekannten Gleichung:
Gleichung 1: Vereinfachte Berechnungsvorschrift für Wärmeausdehnung
Hier bedeuten:
ΔL = Temperatur bedingte Längenänderung [mm]
∝ = Längenausdehnungskoeffizient [K-1]
L0 = Ausgangslänge (ohne Toleranz!) bei Normtemperatur (20 0C) [mm]
ΔT = Temperaturveränderung [K]
Somit gibt es also eine temperaturbedingte Geometrieänderung (Expansion oder Kontraktion) ΔL, die nahezu proportional zur Ausgangslänge L0, zum Längenausdehnungskoeffizienten α als Materialkonstante und der Temperaturänderung ΔT ist.
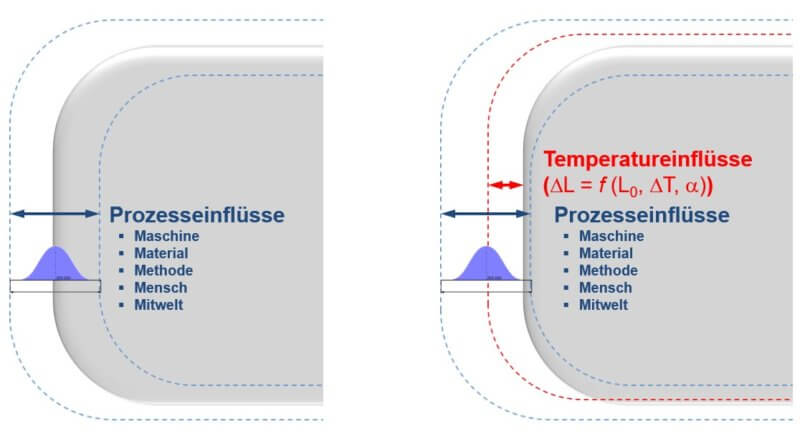
Abbildung 1: Interpretation der Wärmeausdehnung
In der grafischen Darstellung (Abbildung 1) wird deutlich, dass die Temperatureinflüsse auf das Bauteil und die daraus resultierenden Geometrieänderungen (hier Expansion) in Form einer Mittelwertverschiebung die prozessbedingten Einflüsse überlagern.
Relation thermischer bedingter Geometrieänderungen zur Toleranz
Das fertigungsbedingte Abweichungen unvermeidbar sind und diese im Rahmen der Konstruktion mit der Vergabe von Toleranzen erfasst werden, ist gängige Praxis. Es sollten darüber hinaus aber auch thermische Einflüsse bei der geometrischen Absicherung von Baugruppenfunktionen berücksichtigt werden? Diese Frage generierte die Anschlussfrage, in welchem Verhältnis sich die Größenordnungen von thermisch bedingten Geometrieänderungen gegenüber den Toleranzen bewegen?
Der nachfolgende Graph (Abbildung 2) zeigt unter Berücksichtigung des vereinfachten linearen Ansatzes (Gleichung 1), wie sich das Verhältnis der temperaturbedingten Längenänderung zur Toleranz (ΔL/T) mit zunehmender Temperaturdifferenz (ΔT) ändert. Basis dieser Betrachtung ist eine konstante Ausgangslänge (L0), die mit einer ebenfalls konstanten Toleranz von 0,46mm (gemäß DIN 16742, zukünftig ISO 20457 für Kunststoffformteile) berücksichtigt wird. Die Relevanz der thermischen Einflüsse dominiert, wenn das Verhältnis 1:1 überschritten wird. In diesem Graph (Abbildung 2) werden die Abhängigkeiten für unterschiedliche Kunststoffe und Metalle gezeigt.
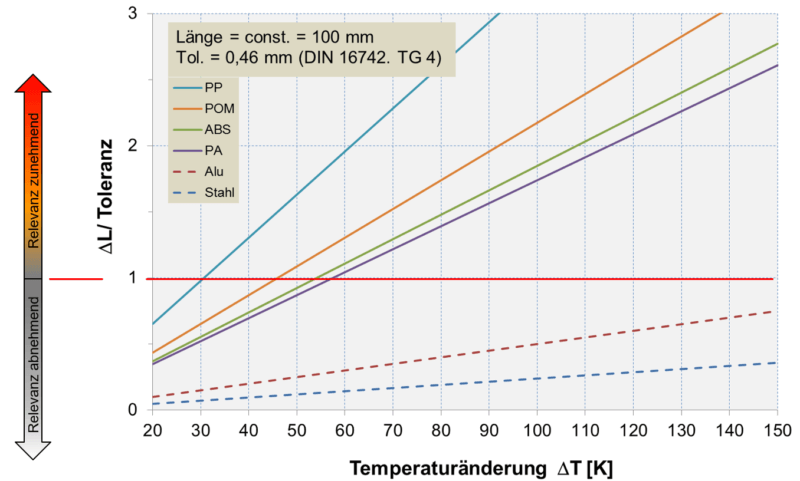
Abbildung 2: Relevanz der thermischen Effekte in Abhängigkeit der Temperaturdifferenz
Deutlich wird, dass schon bei moderaten Temperaturdifferenzen von 30 bis 60 [K] bei den Kunststoffformteilen das Verhältnis in der Gewichtung der Abweichungen zu Ungunsten der thermischen Einflüsse kippt. Die thermisch bedingten Einflüsse werden ab dieser Schwelle größer, als die vorgesehenen Toleranzen.
Um vergleichend einen Eindruck davon zu bekommen, wie die geometrischen Dimensionen auf die schon zuvor beschriebene Verhältnismäßigkeit (ΔL/T) wirken, wird nun die Temperaturdifferenz ΔT = 80 [K] konstant gehalten und die Ausgangslänge L0 [mm] variiert.
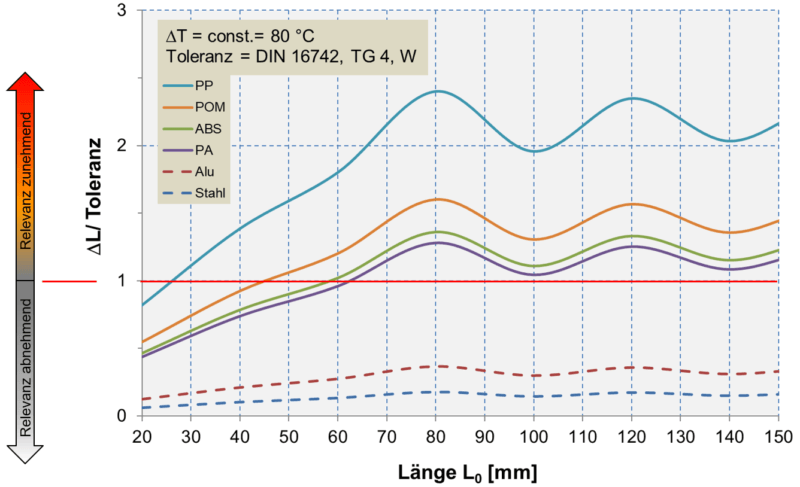
Abbildung 3: Relevanz der thermischen Effekte in Abhängigkeit der Ausgangslänge
Auch in diesem Graph (Abbildung 3) wird deutlich, dass insbesondere die Kunststoffformteile bei schon kleinen Dimensionen 30 bis 50 [mm] im Verhältnis zur Toleranz relevante Längenänderungen erfahren. Die wellenförmigen Verläufe mit steigenden Ausgangslängen resultieren aus dem nicht linearen Verlauf der entsprechenden Allgemeintoleranzen für Kunststoffformteile.
Für die Praxis bedeutet dies, dass schon bei moderat zu erwartenden Temperatureinträgen deren Einflüsse bei der geometrischen Absicherung schon im Entwicklungsprozess Berücksichtigung finden sollten. Und dies gilt nicht nur für groß dimensionierte Bauteile, sondern auch für kleinere, wie Sie häufig in medizintechnischen oder elektromechanischen Anwendungen zu finden sind.
Thermisch Einflüsse auf die Baugruppenfunktion
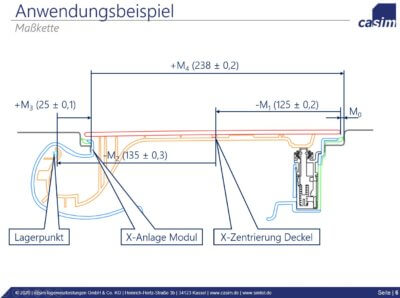
Bisher wurde thematisiert, dass Werkstoffe der thermischen Ausdehnung (Expansion, Kontraktion) unterliegen und dass sie in Zahlen ausgedrückt sehr schnell in die Größenordnung der vergebenen Toleranzen und darüber hinaus zum Liegen kommen. Diese Abhängigkeiten sollen nun im Wirkverbund einer Baugruppe betrachtet werden. Zur Verdeutlichung der Zusammenhänge soll folgende einfache Baugruppe, bestehend aus zwei Einzelteilen, dienen. Untersucht werden soll, wie sich der Funktionsspalt M0 in Abhängigkeit von den temperaturbedingten Einflüssen auf die Geometrien verändert. Der Funktionszusammenhang wird, wie in Abbildung 4 zu sehen, über eine Maßkette beschrieben. Hierbei steht Maßkettenglied M1 für die Länge des eingelegten Bauteiles mit der Nominallänge N01. Maßkettenglied M2 beschreibt die Bereite des Ausschnittes mit der Nominallänge N02. Bei linksseitiger Anlage des eingelegten Teils ergibt sich dann der Funktionsspalt M0, dass sogenannte Schließmaß. Dieser hat die Nominalweite N0.
Ändert nun das Einlegeteil seine Dimensionen, ändert sich der Funktionsspalt M0. Wird N01 zum Beispiel größer, wird der Funktionsspalt M0 im gleichen Maße kleiner. Für die Breite des Ausschnittes sind die Abhängigkeiten genau umgekehrt. Eine Vergrößerung des Ausschnittmaßes N02 führt also zu einer entsprechenden Vergrößerung des Funktionsspaltes.
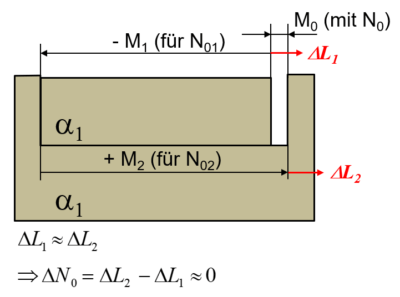
Abbildung 4: Baugruppe mit Einzelteilen aus gleichem Material
Unter der Annahme, dass beide Bauteile aus dem gleichen Material bestehen (dargestellt durch den gleichen Wärmeausdehnungskoeffizienten a1) und der gleichen (Baugruppen-)Temperatur unterliegen, gilt, dass die temperaturbedingte Längenänderung ΔL1 nahezu gleich ist mit ΔL2. Dass heißt, dass im nahezu gleichen Maße, wie das Einlegeteil zum Beispiel größer wird auch der Ausschnitt zunimmt. Obwohl beide Bauteile womöglich eine beträchtliche Wärmeausdehnung erfahren, hat dieser Umstand keinen relevanten Einfluss auf die Baugruppenfunktion – die Einzeleffekte heben sich gegenseitig auf.
Das obige Beispiel wird nun der Art variiert, dass beide Einzelteile aus unterschiedlichen Materialien bestehen. Alle anderen Parameter des Modells sind unverändert.
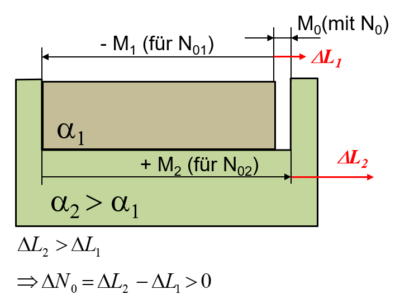
Abbildung 5: Baugruppe mit Einzelteilen aus unterschiedlichen Materialien
In diesem Szenario ergibt sich, dass die temperaturbedingte Längenänderung ΔL1 und ΔL2 unterschiedlich sind. Wenn α2 größer ist als α1, resultiert daraus, dass ΔL2 ebenfalls größer als ΔL1 ist. Somit ändert sich der Funktionsspalt also im relevanten Maß, wenn die Baugruppe im Betrieb mit Temperatur beaufschlagt ist. Jedoch wird hier nicht die Längenausdehnung der Einzelteile im vollen Umfang wirksam. Vielmehr kommt nur eine resultierende Ausdehnung zum Tragen, die sich als Differenz aus ΔL2 und ΔL1 ergibt.
In der Baugruppe können sich die temperaturbedingten Einflüsse auf die Geometrien, selbst wenn sie in relevanter Größe auftreten, im besten Fall eliminieren. Dies ist der Fall, wenn die Einzelteile einer Baugruppe aus dem gleichen Material bestehen und die geometrischen Verhältnisse vergleichbar sind. Für die Praxis bedeutet dies, dass unter diesen Umständen eine Berücksichtigung der thermischen Verhältnisse zur geometrischen Absicherung der Baugruppenfunktionen nicht erforderlich ist.
Hat man es aber mit hybriden Baugruppen zu tun, also mit solchen aus unterschiedlichen Materialien, kompensieren sich die thermischen Einflüsse auf die Geometrien nicht mehr und können somit schnell Größenordnungen annehmen, die über denen der Toleranzen liegen. Hier sollten bei nennenswerten Temperatureinflüssen unbedingt entsprechende Berechnungen vorgenommen werden.
Überlagerung von fertigungsbedingten und thermischen Einflüssen in einer Baugruppe
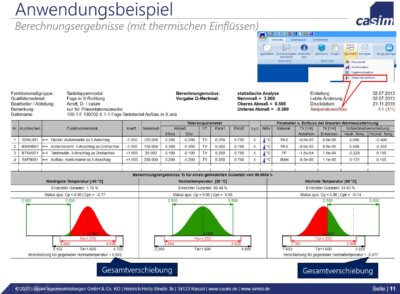
Die Praxis ist in der Regel dadurch geprägt, dass nicht nur ausschließlich fertigungsbedingte Abweichungen auf Baugruppenfunktionen wirken. Vielmehr wirken gleichzeitig auch thermische Einflüsse auf die Bauteilgeometrien. Wie überlagern sich die Effekte beider Einflüsse und wie wirken sie sich auf Baugruppenfunktionen aus?
Die soll in einem Berechnungsbeispiel erörtert werden, welches Sie in unserem Downloadbereich finden können. Unter Nutzung der Tolerierungssoftware simTOL wird gezeigt, wie durch ein geeignetes Berechnungsprogramm im Zuge von statistischen Toleranzberechnung diese Frage schnell und sicher beantwortet werden kann.