Beispielrechnung (1): Axiale Wellenlagerung

Problemstellung

Gesucht wird der „Lagerspalt zwischen Rillenkugellageraußenring und Lagerdeckelstützring“ auf der Festlagerseite, wie in Abbildung 1 dargestellt.

Die Kundenforderung beträgt für den axialen Lagerspalt 0 +0,6/+0,1 [mm]. Dementsprechend ist ein Kleinstspalt von 0,1 [mm] und ein Größtspalt von 0,6 [mm] einzuhalten.

Ziel der Analyse

Ermittlung des tatsächlichen Istzustandes
Ermittlung der Einflussgrößen bei gegebener Serienfertigung
Ermittlung der Prozesssicherheit der Kundenforderung für das Spaltmaß; gefordert werden Cp > 1,33 und Cpk > 1,33

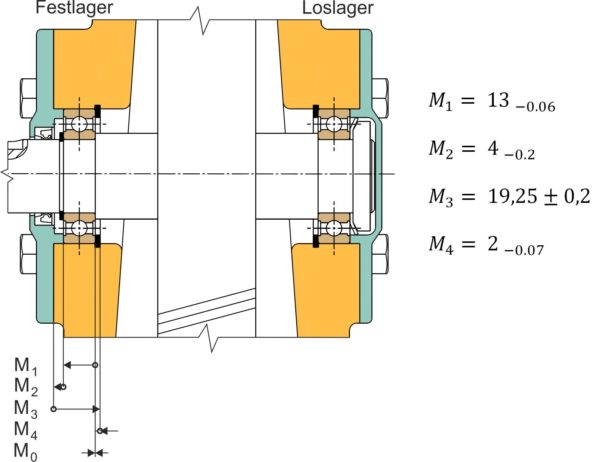
Abbildung 1: Direkte Funktionsmaße an einem Stirnradgetriebe

Produktparameter (tolerierte Maße)

M1: Einreihiges Rillenkugellager: Ringbreite
M2: Gehäusedeckel (festlagerseitig): Axiales Stufenmaß des Deckelstützrings
M3: Gehäuse (festlagerseitig): Axiale Stellung des Nuteinstiches für Sicherungsring (rechte Seitenfläche) zu Deckelanschraubfläche
M4: Sicherungsring: Breite

M1: 13 -0,06 [mm]
M2: 4 -0,2 [mm]
M3: 19,25 ±0,2 [mm]
M4: 2 -0,07 [mm]

Prozessparameter (Prozessverteilung VT)

VT1: Normalverteilung mit Cp = 1,33 und Cpk = 1,33
VT2: Trapezverteilung mit Cp = 1,04 und Cpk = 1,04
VT3: Trapezverteilung mit Cp = 1,04 und Cpk = 1,04
VT4: Normalverteilung mit Cp = 1,33 und Cpk = 1,33
Hinweis:
Trapezverteilungen berücksichtigen fertigungstechnische Abweichungen von den statistischen Idealbedingungen wie:

Mittelwertverschiebung, z.B. durch unkorrekte Werkzeugeinstellung,
asymmetrische (schiefe) Verteilung, z.B. bei Positionstoleranzen,
Mischverteilung (1. und 2. Art), z.B. durch unterschiedliche Fertigungsstandorte und/oder Prozesstrend, z.B. bei kontinuierlichem Werkzeugverschleiß.

Richtungs- und Linearitätskoeffizienten

Koeff. 1
-1 (negatives Maßkettenglied)
Koeff. 2
-1 (negatives Maßkettenglied)
Koeff. 3
1 (positives Maßkettenglied)
Koeff. 4
-1 (negatives Maßkettenglied)

Funktionszusammenhang der Maßkettenglieder

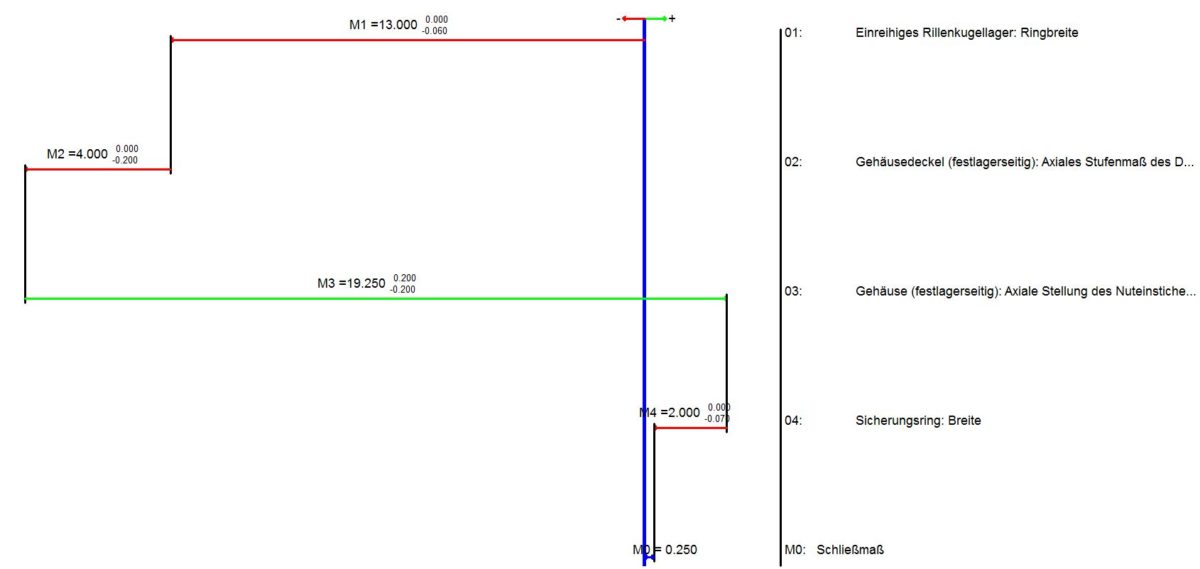
Abbildung 2: Maßplan bzw. Maßkettenstruktur der positiven und negativen Maßkettenglieder (Analyse mit dem Programmsystem simTOL)

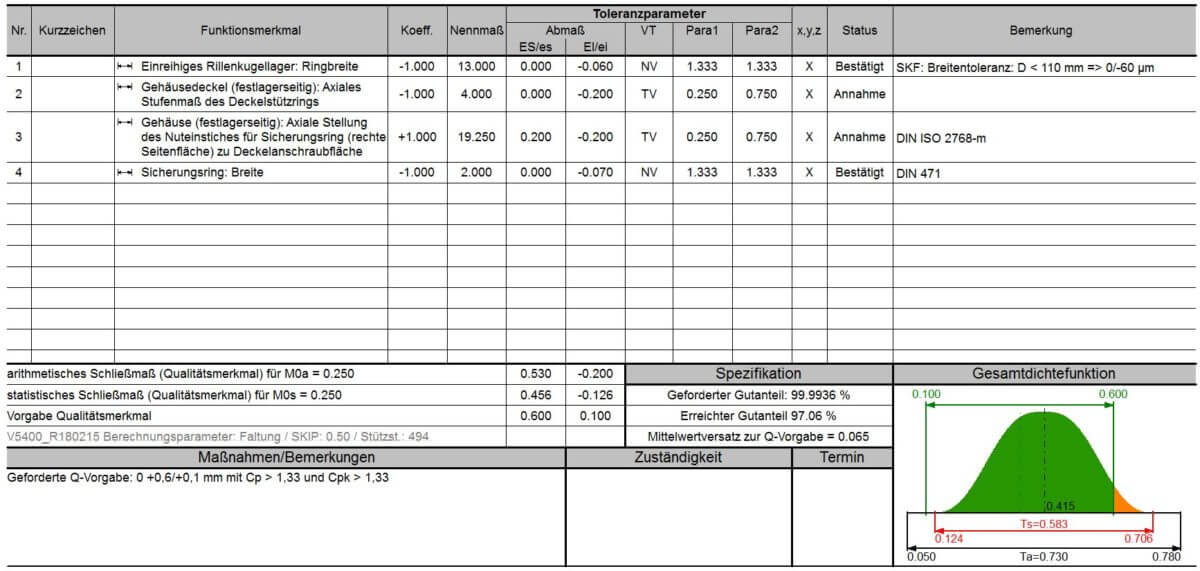
Berechnungseingabe und Ergebnis

Das Ergebnis zeigt einen arithmetischen Minimalspalt von 0,05 [mm] und einen arithmetischen Maximalspalt von 0,78 [mm]. D.h., es tritt keine Kollision auf.

Das statistische Toleranzanalyseergebnis zeigt einen Minimalspalt von 0,124 [mm] und einen Maximalspalt von 0,706 [mm] bei Pa = 99,9936 [%.]

Abbildung 3: Ergebnisübersicht (Analyse mit dem Programmsystem simTOL)

Prozesssicherheit der Kundenforderung

Das Ergebnis zeigt bezogen auf die Kundenforderung von 0,1 [mm] Kleinst- und 0,6 [mm] Größtspalt, dass diese Forderung nur zu 97,06 [%] erfüllt wird.

Dementsprechend ist die Kundenforderung unter den hier festgelegten Prozessqualitäten nicht prozesssicher darzustellen.

Beeinflussende Maßkettenglieder

Die Paretoanalyse zeigt mit den blauen Balken den artihmetischen Einfluss eines jeden Maßkettengliedes auf den hier zu berechnenden Luftspalt. Und mit den roten Balken den statistischen und damit realen Einfluss.

Abbildung 4: Paretoanalyse (Analyse mit dem Programmsystem simTOL)

Aus der Paretoauswertung wird ersichtlich, dass mit 79,0 [%] die axiale Stellung der Nut am Getriebegehäuse den signifikanten Einfluss auf den Luftspalt ausübt. Und mit nur 0,5 [%] die Ringbreite des Rillenkugellagers einen sehr geringen Einfluss ausübt.

Optimierungsansatz

Ein möglicher Optimierungsansatz ist mit Hilfe der Paretoanalyse in der Identifizierung des Hauptbeitragsleister gegeben. Hiernach sollte die Toleranz t3 der axialen Stellung der Nut am Getriebegehäuse eingeengt werden.

Umsetzung:
M1: 19,25 ±0,2 [mm] auf
M1 (neu): 19,25 – 0,2 [mm]

Informieren Sie sich jetzt über unsere Leistungen

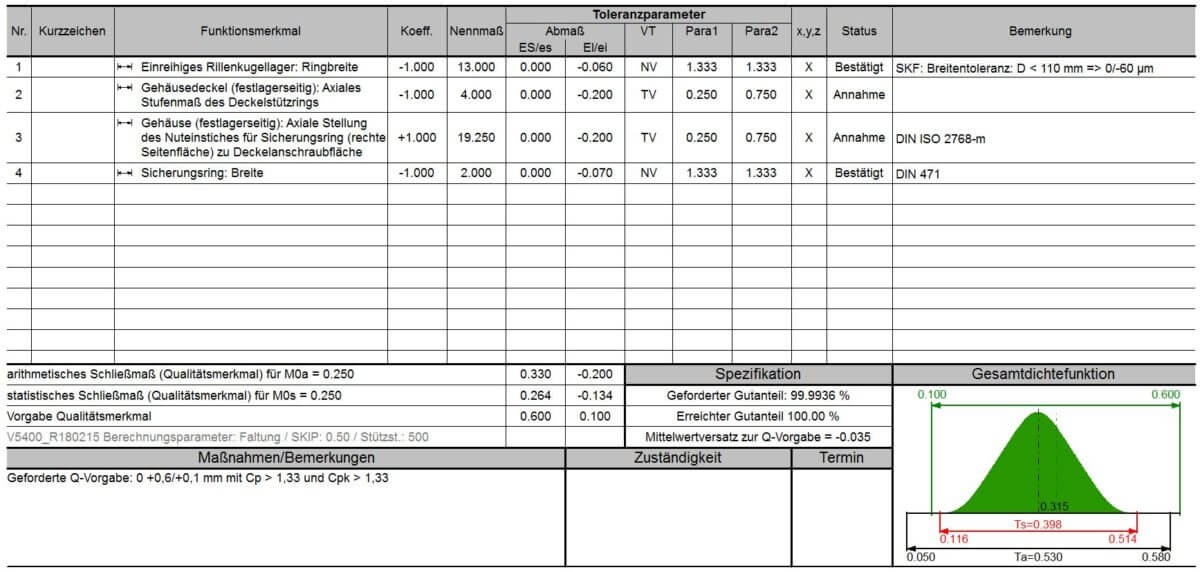
Berechnungseingabe und Ergebnis für den optimierten Zustand

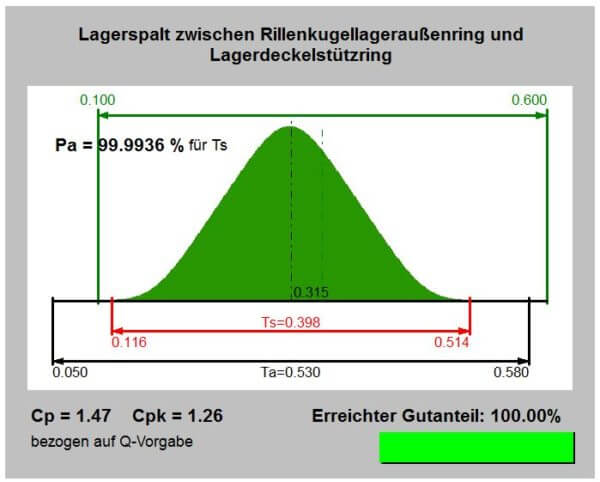
Abbildung 5: Ergebnisübersicht optimierter Zustand (Analyse mit dem Programmsystem simTOL)

Prozessicherheit der Kundenforderung

Das Ergebnis zeigt bezogen auf die Kundenforderung von 0,1 [mm] Kleinst- und 0,6 [mm] Größtspalt, dass diese Forderung zu 100 [%] erfüllt wird.

Der Nachweis mittels der Prozessfähigkeitsindizes nach DIN ISO 22514 ergibt:

Prozessfähigkeitsindex Cp:
Cp = T/(Q(0,99865) – Q(0,00135))
Cp = 0,5/(0,485 – 0,145) = 1,47

T = Toleranz für gefordertes Spaltmaß
Q(0,99865) = oberes Quantil
Q(0,00135) = unteres Quantil

Kleinster Prozessfähigkeitsindex Cpk:
Cpk = (µ – USG)/(µ – Q(0,00135))
Cpk = (0,315 – 0,1)/(0,315 – 0,145) = 1,26

µ = Mittelwert der Schließmaßverteilung
USG = untere Spezifikationsgrenze für gefordertes Spaltmaß

Dementsprechend ist die Kundenforderung zum größtenTeil erfüllt. Der Prozessfähigkeitindex ist Cp = 1,47 (prozessfähig) und der kleinste Prozessfähigkeitindex ist Cpk = 1,26 (bedingt beherrscht).